199: Text, Subtext and Context (Theodore Roosevelt & the Panama Canal)

1-sources

 

2-what

 

Screen Shot 2016-05-13 at 2.56.54 PM

 

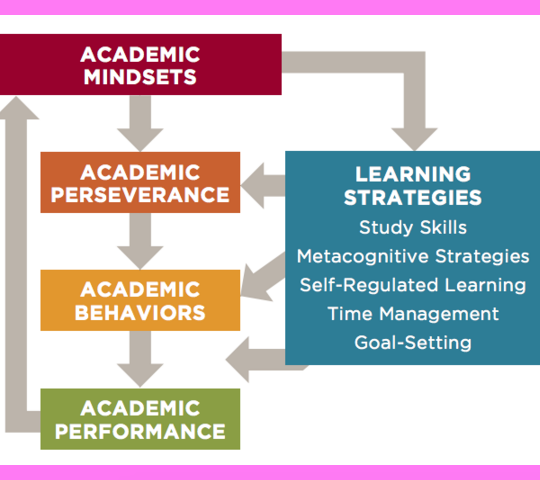
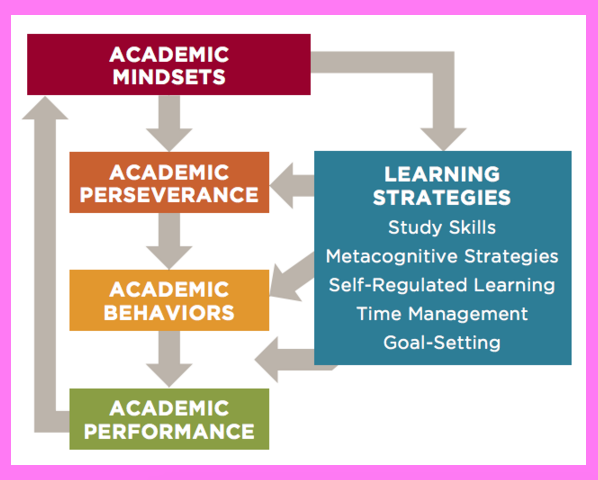
A Common Language for Investigating the Part:
  • Using content, context and sub-text to summarize and evaluate historical sources can work for all units
  • Need to repeatedly use content, context and sub-text reflections to build up student skills
  • For guided questions related to content, context and sub-text, go this article: Making historical thinking a reality
Criteria for Selecting Sources
  1. Do not use more than 4 to 6 sources.  Especially in the beginning.
  2. Read the sources ahead of time and check for:
    • can lead to discussion related to driving question
    • accessible to students
  3. Vary types of sources
    • examples: cartoons, artwork, pictures, text, pop culture sources, maps, data tables, graphs, etc
  4. Aid students with:
    • academic vocabulary
    • contextualizing sources
    • providing legible copies of sources (if they are originally in cursive)
  5. Make sources of comparable length if you are using the jigsaw strategy to distribute / share sources.
Initiating the Investigation
  • Investigate sources and look for:
    • lies,
    • half-truths
    • exaggerations
    • rationalizations
    • obfuscations
    • Math / Science adaptations:
      • Look at strategies or concepts and identify
        • Always true
        • Sometimes true
        • Always false
        • Sometimes false
  • Students read excerpt from Theodore Roosevelt’s autobiography about the Panama Canal and ponder the Driving Question
    • What is Roosevelt doing in his autobiography (lying, telling a half-truth, exaggerating, rationalizing or obfuscating)?
    • What role did the US play in the acquisition of the territory used to construct the Panama Canal?
    • Math / Science adaptations:
      • Could present or develop circle axioms (or other conjecture types) and ask:
        • are these always, never or sometimes true?
        • In what situations are they true?
Digging Deeper
  • Students in teams are given one historical source and asked to answer questions related to the content, context and subtext of the source
    • source represent a cross section of view about the Panama Canal
    • 2 short guide questions:
      • What role did US play in the Panamanian Revolution?
      • Is there any info in this source that challenges assertions in Theodore Roosevelt’s autobiographical excerpts?
  • Students in teams discuss their sources.
    • Each team member read and analyzed different source
    • Discuss different sources citing specific examples and quotes from their sources
  • Alternatives to jigsaw approach:
    • One person reads all sources – very time consuming
    • Each group of 3 or 4 analyzes the same source and presents their findings to the class so whole class is exposed to all sources
    • Math /  Science Connection
      • Jigsaw approach – Each person in the team examine a different piece of evidence and share interpretations, observations with whole team (all evidence relates to the same concept)
      • Non-jigsaw approach – All students in same team of 2-3 solve the same problem – challenge students to develop multiple approaches to the same problem and use visuals to represent different approaches
Doing Source Work:
  • Wineburg, Historical Thinking Matters Framework
    • sourcing
    • contextualizing
    • close reading
    • corroborating
  • Hicks, et al. SCIM-C Strategy Framework
    • summarizing
    • contextualizing
    • inferring
    • monitoring
    • corroborating
  • In both approaches:
    • students need to move beyond a single source
    • examine relationships provided by each piece of evidence
    • Corroboration phase -> legitimate interpretations of historical questions
  • Math / Science connections:
    • Math framework
      • Asking questions
      • Making models to answer questions
      • Computations
      • Relating model results back to real life to check if they apply
    • Science framework
      • Making observations
      • Asking questions and hypotheses based on observations
      • Designing data procedures
      • Gathering, organizing, analyzing data
      • Drawing conclusions
    • Corroboration connections:
      • In Math – verifying that multiple approaches led to the same solution
      • In Science – verifying that different tests yield the same results
Complicating the Investigation
  • Students corroborate their evidence by completing the following sentence stem:
    • The various types of sources used to determine the purpose of Roosevelt’s autobiography created problems because …
    • Math connections
      • The various ways of representing the problem reveal different facets of the problem including …
      • The various ways of solving the problem are good for different purposes including …
    • Science connections
      • The various data sources yield different conclusions because …
      • The various data sources create problems because …
  • Types of student responses:
    • unreliable due to biased subtexts
    • sources only try to portray their own biased viewpoints
    • hard to know which source to believe
    • contradicting viewpoints, hard to tell what really happened
  • Student difficulties:
    • Students struggle to make connections among content, context and subtext
  • Another question that guides student corroboration of various sources: The subtext of the various documents was important to consider because …
    • Math / Science connection
      • The contexts / subtexts of the data are important to consider because …
    • Student responses:
      • explains why the source was written
      • explain variety of opinions
      • explains variety of evidence used by sources
      • helped convey reliability of sources
      • insights into intentions of authors
      • helped to tease out truth in sources
      • helped show biased in sources
  • “Overall when trying to interpret events from the past, you need to …”
    • Math / Science connection
      • Overall, when trying to interpret data, you need to …
    • Student responses
      • consider sources with different viewpoints
      • research background info that reveals subtexts of sources
      • compare information from different sources
    • Student difficulties
      • believe that bias negates validity of a source (mathematical approach to history)
Student Interpretations – Transition Quick Write
  • Transition quick write at end of day one: Attempt to answer the driving question
    • Look fors in student quick writes:
      • evidence from sources
      • perspectives from multiple sources
    • Math / Science connection
      • Use driving question as quick write prompt
    • Student difficulties
      • Using evidence
      • Bridging content, context, and subtext in interpretations
      • Mathematical approach to history (problematic approach)
        • require consensus among sources
        • require lack of bias in sources
Returning to the Investigation:
  • End analysis by revealing most controversial and faceted source to students
  • Math / Science connection
    • Could reserve most nuanced and controversial piece of data for release near middle or end of project
Conclusions:
  • Analyzing sources’ content, context and subtext can help student investigate the past rather than just memorize and regurgitate text excerpts
  • Teacher resistance
    • kids can’t do this work
      • responses
        • studies have shown that this type of work can be done by elementary school students
        • teacher perseverance helps students acquire student skills
        • historical investigations make history more interesting
        • prepares students with skills they can use in any career
3-sowhat
Finding the right evidence and fashioning the right driving question can make boring topics interesting to students.  Releasing evidence at various points in the project can start and reinvigorate conversations related to the driving question.  Using content, context and subtext to analyze evidence can teach students how to investigate, question and interpret evidence.

 

4-nowwhat
Preparation Steps
  • Collect evidence (data, sources, etc) that students can use to explore content by investigating a driving question
  • Design driving question
  • Design thinking sheets that help students examine content, context and subtext of sources
  • Design prompts to facilitate conversations that corroborate evidence – see above for examples.
Early Implementation Steps
  • Use a controversial or provocative source to introduce a driving question
  • Assign sources (various) to students working in teams
  • Individually assign students to examine the content, context, and subtext to different sources within a team.
  • Get students to answer prompts as a team that get them to corroborate their sources and formulate interpretations that address the driving question
Advanced Implementation Steps
  • Gather evidence and sources that uncovers current problems that relate to central concepts in your course. Design project and driving questions around that set of sources.

 

5-relatedstuff

167: Assessing Skill in Application & Performance (1 of 2)

2-what
Screen Shot 2016-05-08 at 10.30.46 PM
  1. Directed Paraphrasing
    • Description
      • Students paraphrase a part of a lesson for a specific audience
    • Purpose
      • Assess student ability to explain concepts in their own words
      • Assess how well students have internalized content
    • Step-by-Step Procedure
      • Select an important concept, topic, theory, etc that has been covered in class and that has outside classroom implications.
      • Determine a hypothetical realistic audience for a summary of the topic.
      • Try out directed paraphrasing for selected topic and audience.
      • Assign directed paraphrasing.  Be sure to explain;
        • the topic
        • the audience
        • purpose of the summary
        • length and time limits
    • Analysis Steps
      • Divide up responses into 4 piles: confused, minimal, adequate, excellent.
      • Determine common characteristics of the 4 piles in regards to
        • accuracy of the paraphrase
        • suitability for intended audience
        • effectiveness in fulfilling its purpose
      • Circle the clearest and muddiest points in each paraphrase
    • Extension Ideas
      • Direct students to create directed paraphrases on the same topic for 2 different audiences with associated different purposes.
      • Ask students to keep a journal of directed paraphrases to summarize important topics in the course
      • Jigsaw readings and have students develop paraphrases to summarize these and then share them with students who analyzed different texts.
      • Get an appropriate expert that represents the audience to give feedback on the directed paraphrases.
      • Provide handouts with successful examples.
      • Give students warm and cool feedback on their responses.
    • Pros
      • Builds up students ability to comprehend and communicate content
      • Teachers can assess quickly if students understand content and make adjustments to future lessons
      • Emphasizes the relevance of specific concepts
    • Cons
      • Without strict length limits, these can be time consuming to create
      • Hard to establish good qualitative criteria for these
      • Paraphrasing skills can not improve without focused descriptive feedback.
    • Caveats
      • Select appropriate audiences in order to enhance the relevance of the assignment
      • First attempts may not include adjustments for selected audience
      • Use more than once so that teachers and students can learn from the process
  2. Applications Cards
    • Description
      • On an index card or small slip of paper, students provide a real world application for a selected topic
    • Purpose
      • Tie new knowledge (selected topic) with prior knowledge to create possible applications
      • Assess how well students understand and can apply content
    • Step-by-Step Procedure
      • Identify an important topic just studied in a course that has real world applications
      • Decide how many examples (1 to 3) and how much time (3-5 min) you will give students for this task
      • Assign task and hand out cards.  Emphasize that you are asking for “fresh” applications – not the ones mentioned in class.
      • Collect cards and let students know when they will receive feedback
    • Analysis Steps
      • Divide responses into 4 piles – great, acceptable, marginal, not acceptable
      • Find common characteristics of responses in each pile
      • Share 3 to 5 good examples and 1-2 marginal examples with the class.  Try to pick a selection that is varied.  Explain why good examples are accurate and why marginal examples are implausible.
    • Extension Ideas
      • Let students work in small groups to come up with application ideas
      • Encourage students to keep an applications journal – 2 min at end of each class brainstorming possible real world application of concepts covered that day
    • Pros
      • Simple way to gets students thinking about possible uses of what they are learning
      • Tying prior knowledge to content to create new applications creates memorable associations
      • Possibility of real world applications can get students more engaged in the course
      • Students can benefit from hearing about the best examples of applications (even more so than textbook examples)
      • Teachers get access to a new bank of applications to use in class examples
    • Cons
      • Can shift focus of class to more concrete level than teacher intends
      • Students not interested in applications may not see the point in this
      • Not all fields have easily definable real world applications
    • Caveats
      • Students who suggest bad examples may learn misconceptions from these.  Provide feedback to correct these misconceptions.
      • Engagement in examples may eat up more class time than intended
  3. Student-Generated Test Questions
    • Description
      • Students create model test questions and the correct responses to these
    • Purpose
      • Teachers can see what students think is the most important and most fair content to assess
      • Teachers can see how well students can answer their own questions
      • Teachers can adjust students’ expectations of the course if these prove to be unrealistic
    • Step-by-Step Procedure
      • Analyze an upcoming test to determine the types of problems it will include.
      • Write out specs for questions that will direct students to create test questions that align to the types of problems that will actually appear on the test
      • Decide how many questions students will generate (1 to 2 is plenty)
      • Explain what you want students to do, the purpose for it, when they will get feedback and how doing this will improve their performance on the upcoming test
    • Analysis Steps
      • Note the following for each:
        • topic
        • thinking level
        • clarity
        • difficulty
      • Look for helpful patterns in the categories above – what’s included? what’s missing
      • Share observations with the class – especially if the difficulty and thinking levels of their questions is lower than the expectations of the source
    • Extension Ides
      • Let students come up with questions in pairs or small groups.
      • May want to assign specific topics to specific groups in large classes – can do this alphabetically
      • Offer handout of student generated questions for test review and tips for how to prepare for the upcoming test
      • If the students are pre-service teachers – give them more specific feedback on their question design – especially on the thinking levels they used.
    • Pros
      • Students learn what they understand and not
      • Predicting test questions is a form of test preparation
      • Can avoid ugly surprises due to mismatches in students’ and teacher’s expectations of the course
    • Cons
      • Student who lack experience in creating questions may need to have this modeled.  May need trigger words or sentence stems to create good questions.
      • Students may try to get teacher to put easy questions on the test.
      • Some students may be disappointed if their questions are not included on the review or test.
    • Caveats
      • Do NOT promise to include student test questions on the actual test.
      • Unless students understand the purpose of the assignment, may view this as a thinly veiled attempt to get students to do teacher work.
      • May need to offer some grading credit to the assignment if creating it is time consuming.

 

3-sowhat
Applications cards and directed paraphrasing are assessments that build the connections between content and real world applications and audiences.  Creating these connections may get students to use their prior knowledge and content knowledge in ways that create memorable associations.  Tying content to real audiences and real products can get students more engaged in the content.

 

The student-generated test questions can help students start preparing for high stakes tests.  Analyzing students responses can help teachers become more aware of how his or her expectations match (or don’t match) the student’s expectations. Knowing this in time can help teachers make adjustments to lessons that help those expectations converge in time for the exams.

 

4-nowwhat
Preparation Steps
  • Analyze how learning targets connect with real products and real audiences.  Determine whether or not these relationships are engaging and important.
  • Select a strategy that emphasizes the type of connection between content and the real world (via audience or via product) that is the most engaging and helpful.
  • Create a model of the selected strategy.
Early Implementation Steps
  • Explain the expectations, purpose and criteria for the selected assessment.
  • Walk students through a sample assessment and describe the types of thinking that went into creating the model.
  • Assign the selected assessment.
  • Analyze the selected assessment using some of the analysis procedures described above.
  • Share key findings of assessment analysis with the class.
Advanced Implementation Steps
  • Expand the scope of the assessment using some of the extension suggestions describe above.
  • Expand the assessment into a Quick Writes or Writing to Learn activity.
5-relatedstuff

157: During Reading Activities (1 of 2)

1-sources

 

2-what

 

Screen Shot 2016-05-09 at 12.06.25 AM

 

For part 2 of During Reading Activities, go here.
  1. Partner Reading
    • Focus
      • Sharing ideas, Discussing, Debate
    • Description
      • Partners side by side take turns reading a content-area text
      • Take turns per paragraph
      • In between paragraph discuss what they just read
      • This can be a warmup that transitions to individual silent reading
    • Why Use It?
      • Build up to more independent reading
      • Can help students understand dense texts
      • Can support students who are not year ready for careful independent reading
    • How Does It Work?
      • Select important chunk of content-area text and set aside 5-10 minutes of classroom reading time
      • Form pairs of students who can work together and have similar reading levels
      • Use a volunteer to act as a co-model while you model the strategy for the class.  Model reading aloud, taking turns at paragraphs, and pausing between paragraphs to discuss the text
      • Possible Discussion questions:
        • What did the author say?
        • What were the big ideas?
        • Were there some hard words?
        • Is there anything we didn’t understand?
        • How can we figure it out?
        • What questions do we have?
        • What do you think we will come up with in the next paragraph?
      • After demo, let pairs begin reading. Circulate around the room and observe the pairs at work.   Coach pairs as needed.  Note patterns of confusion and address these in later lessons.
      • At close of activity, ask several pairs to share what their understandings and questions of the text.
    • Variation
      • Students can read in unison and discuss texts in between paragraphs
      • Students can read silently and discuss texts in between paragraphs
    • Related Reading
  2. Post-It Response Notes
    • Focus
      • Reading as Thinking
    • Description
      • Students periodically pause while reading text to think and react to text
      • Record thoughts and questions on post-it-notes
      • Post-it notes can be used in later discussions and writing assignments
    • Why Use It?
      • Helps readers slow down, focus and notice important parts of text
      • Creates concrete notes that can be referred to later
      • Can be rearranged to show different relationships among ideas in text
      • Relaxing form of note taking because post-its are small, readers/writers can see they don’t need to write a lot
    • How Does It Work?
      • Model how to use text with a short passage (~2 paragraphs)
        • notes for confusing points
        • notes for surprising points
        • nots to summarize key points
      • Let students try out strategy.  After several minutes of using the strategy, encourage students to turn their neighbor and discuss their notes.
      • Discuss the post-its with the whole class.
        • Can call on feedback related to key points by asking for post-its at specific locations in the text (bottom of page 3)
        • Ask questions to pull out key elements of the text – conflicts, debates, main ideas, confusing points, surprising points, etc
      • Can also have students bring their notes to a common whiteboard area and group notes under key categories such as: main idea, conflict, confusing points, etc
      • Prior to transferring notes out of book, have students write their name on post-its and the page #
    • Variation
      • Color code notes to distinguish between different types of responses such as summaries, questions, etc
      • Use chart paper to divide up post-its into different categories
      • Use summary notes and quotes to write a paragraph summary of the text.  See Writing to Learn articles and Quick Writes articles for even more ideas.
      • Can use Post-Its as Admit or Exit Slips
  3. Annotating Text
    • Focus
      • Reading as thinking
      • Making connections to other texts, information and self
    • Description
      • Students take notes on key, puzzling, surprising points in the text in the text margins
    • Why Use It?
      • Teaches active reading processes: stop, think and react
      • Practice generating questions from the text
    • How Does It Work?
      • Model how to use the strategy with a short passage.  Think aloud as you mark up the margins to show how to stop, think and react to text excerpts.
      • Ask students to categorize model feedback according to types such as
        • questions
        • connections
        • visual images
        • important parts
        • predictions
        • times I got lost
        • wow factors
        • authors’ style, point of view
      • Have students implement strategy with the above list of types of feedback in view.  Encourage students to stop and think at points that go with all the categories listed above.
      • Provide many opportunities for students to develop their annotation skills over time
    • Variation
      • Have students read and annotate text while assuming a content-specific point of view such as a famous scientist, historical figure, etc (Point of View Annotation)
      • (Conceptual Annotation) have students to watch for specific conceptual groupings while taking notes.  For best results, limit categories to 3 or 4
        • Example of concept groups: causes of concussions, symptoms of concussions, treatment of concussions, prevention of concussions
    • Related Reading

 

3-sowhat
Teaching students how to actively process texts while reading them can help them grow into smarter readers who know to stop, think and react to texts.  Helpful reactions to texts include noticing key points, surprising points, and confusing points and generating related questions and predictions.

 

4-nowwhat
Preparation Steps
  • Decide which During Reading strategies will help your students actively and effectively process texts
  • Practice the strategy you’re about to model
  • Select a short passage for the demonstration of the strategy
  • Gather related materials: texts, post-its, chart paper, etc
Early Implementation Steps
  • Model the strategy using a sample text and think aloud protocol
  • Give instructions for strategy and explain how strategy artifacts will be used later
  • Give students opportunities to use the strategy (multiple opportunities for annotation strategies so students can develop skills over time)
  • Facilitate discussions based on strategy artifacts
Advanced Implementation Steps

 

5-relatedstuff

153: Teaching Math for a Growth Mindset

1-sources

 

2-what
Screen Shot 2016-05-09 at 6.49.00 AM

 

Setting Up Classroom Norms:
  • Positive Norms for Math Classes:
    1. Everyone can learn math to the highest levels.
    2. Mistakes are valuable.
    3. Questions are really important.
    4. Math is about creativity and sense making.
    5. Math is about connections and communicating.
    6. Depth is much more important than speed.
    7. Math class is about learning, not performing.
  • In small groups, lets students specify norms for things they’d like to see / hear / experience (or not) while team problem solving.  Create posters of student preferences.
  • Skills to teach:
    • Listening to each other
    • Respecting each other
    • Building on each other’s ideas
  • Communicate expectations for what math looks like when teams are actively processing such as:
    • Your group will be successful today if you are …
      • Recognizing and describing patterns
      • Justifying thinking and using multiple representations
      • Making connections between different approaches and representations
      • Using words, arrows, numbers and color coding to communicate ideas clearly
      • Explaining ideas clearly to team members and the teacher
      • Asking questions to understand the thinking of other team members
      • Asking questions that push the group to go deeper
      • Organizing a presentation so that people outside the group can understand your group’s thinking
    • I will be looking for:
      • Learning and working in the middle of the table
      • Equal air time
      • Sticking together
      • Listening to each other
      • Asking each other lots of questions
      • Following your team roles
    • You can use the checklists above to record what you’re observing while students work in teams and to provide them feedback on their teamwork.
Believe in All of Your Students
  • Have high expectations for all students and provide support and positive messaging that helps students believe & demonstrate that they can achieve your high expectations
  • Avoid early tracking
  • Avoid unspoken messages that communicate that you don’t believe is someone’s potential – like only assigning them easy work
Value Struggle and Failure
  • Assign challenging math problems that provide opportunities for struggle and learning mistakes
  • Assign low floor, high ceiling tasks
  • Communicate frequently that struggle and failure are good (failing forward)
  • Break the myth of “effortless achievement”; all achievers worked hard and failed, even geniuses
Give Growth Praise and Help
  • Growth praise and help focuses on strategies and effort, not on ability
  • When students do math problem wrong – start by validating the strategy they used to first tackle the problem before redirecting them to new strategies
  • Instead of breaking down problems for students – ask them to draw the problem and see what ideas come out of that activity
  • When students can handle a little more struggle – respond to their requests for help by saying – Do you want my brain to grow or your brain to grow?
  • Show students that math is a growth subject
Teach Math as an Open, Growth, Learning Subject
  • Closed math problems – just ask for calculations, promote a fixed mindset
  • Open up math problems so they invite students to think and grow.
    • Example of opening up math problems:
      • Closed form:  What is 1/2 divided by 1/4?
      • Open form: Make a conjecture about the answer to 1/2 divided by 1/4 and make sense of the answer by using a visual representation of the solution.
      • Closed form: Simplify (1/3)(2x+15)+8
      • Open form: Find as many ways as possible to represent (1/3)(2x+15)+8 that are equivalent.
      • Closed form:  Find the 100th case.
      • Open form: How is the pattern growing? Use your understanding of the pattern to generalize to the 100th case.
  • Ask students to discuss:
    • ways of seeing mathematics
    • ways of representing ideas
    • different pathways through problems and solutions
    • why use different methods
    • how do different methods work
  • Instead of just finding answers allow students to:
    • explore ideas
    • make connections
    • value growth and learning
    • learn standard procedures when they are ready to see the need for them and can make sense of them
Encourage Students to be Mathematicians
  • What mathematicians do and think:
    • math is creative, beautiful and aesthetic
    • propose and test ideas
    • develop working definitions for ideas based on consensus and reasoning
    • share thinking and ideas
  • Do not be afraid to call students, young mathematicians – why not? if they can be young artists and young musicians, why not young mathematicians?
Teach Mathematics as a Subject of Patterns and Connections
  • Encourage students to see themselves as pattern seekers
  • Teach traditional procedures as one of many sense making approaches to perform operations
  • Encourage students to see math as a classification and study of all possible patterns
  • Give students an active role in pattern seeking
  • Help and let students see the connections between methods
Teach Creative and Visual Mathematics
  • In expectations ask students not for speed, but for creative solutions to problems
  • Engage students by asking them to represent problems visually
  • Connect visual ideas with numerical or algebraic methods / solutions
  • Color code:
    • represent the same ideas (ex: the variable x) using the same color
    • illustrate division by using different colors for partitions (division quilt)
Encourage Intuition and Freedom of Thought
  • Encourage intuition by asking students what they think would work before showing them a method
    • give them opportunities to try their methods on problems before teaching new methods
  • Start with the hypothesis that any subject can be taught effectively in some “intellectually honest” form to a child (Bruner)
Value Depth over Speed
  • Ask questions that are open enough to bring depth into discussions
    • Closed form:  Supplementary angles add up to what number?
    • Open forms: Can two acute angles be supplementary angles?  Can two obtuse angles be supplementary angles?
    • Closed form asks for a single answer.
    • Open form provokes conjectures and discussions.
  • Ask students who finish early to extend problems in any way they wish
  • Aim for depth, not speed – engage students by allowing them to go deeper into problems
Connect Mathematics to the World Using Mathematical Modeling
  • Textbooks oven cast math in pseudo contexts (fake real world problems)
  • Use real world variables part of the time to expose students to real uses of math
  • View math as a posing questions and form math models around those questions
  • Modeling – simplification of any real world problem into a pure math form that can help solve a problem
  • Students often use modeling all the time, but are unaware of it
  • Use visual representations to represent problems (one type of modeling)
  • Use real data from newspapers, magazines, online databases, etc.
  • Make students think about how contexts constrain possible solutions
Encourage Students to Pose Questions, Reason, Justify and Be Skeptical
  • Offer students opportunities to pose questions to situations
    • Example:  Give students priced for finished bracelets and for bracelet supplies.  Then ask them discuss the situation and pose questions.
  • Give students opportunities to try out their own conjectures and use reasoning and data to prove or disprove them.
Teach with Cool Technology and Manipulatives
  • Manipulatives: Cuisenaire rods, multilink cubes, pattern blocks
  • Apps: Geometry Pad (iPad), GeoGebra, Tap Tap Blocks, and many more.  See Rich Mathematical Tasks for ideas.

 

3-sowhat
Teaching mathematics in ways that promote growth mindsets enables students to perceive math as a living, engaging, relevant, and accessible subject.   Giving them access to mathematical processes other than computation, gives students a better chance to experience mathematics more fully and to relate mathematics to processes they already do – such as make conjectures, ask questions, and notice and use patterns. Creating the math culture that promotes growth mindset involves teaching students how to collaboratively problem solve, modeling and teaching more math phases (question formulation, modeling, computation, evaluating models, etc.), designing and facilitating math problems with low floors, high ceilings and authentic contexts, and integrating real world data and technology into problem solving.

 

4-nowwhat
Preparation Steps
  • Design and implement learning activities that promote growth mindset and collaboration norms.  Create visuals to market the ideas that emerge from these activities.
  • Research and design curriculum that includes Rich Mathematical Tasks with low floors, high ceilings, open questions, and engaging (if possible real) contexts.
  • Develop assessment tools that relate to math learning and collaboration processes.
  • Research technology tools and manipulatives that can be used to create and facilitate more rich mathematical tasks.
Early Implementation Steps
  • Implement the curriculum and tools planned above.
  • Use student feedback to adjust learning experiences as needed.
Advanced Implementation Steps
  • Identify helpful strategies that can be incorporated into routines to consistently promote a culture of growth mindset.
  • Collaborate with other math teachers and teachers in related disciplines on norms and strategies that can be used in multiple contexts to cultivate growth mindset.

 

5-relatedstuff

147: Learning Strategies

1-sources

 

2-what
 Screen Shot 2016-04-16 at 9.59.38 AM

 

LEARNING STRATEGIES
  • Involve several processes:
    • metacognition:
      • knowing how to monitor one’s misunderstanding
    • self-regulated learning:
      • intentional use of metacognition to learn
      • selecting strategies and environments most conducive to learning
        • selecting effective strategies can become automatic as students become more expert in specific disciplines
      • monitoring learning processes to adjust effort to meet demands of those processes
      • fighting urge to give up on learning processes
      • multiple phases of self regulation:
        1. judging one’s cognitive abilities (judgment of learning or JOL)
          • seeing connections between current tasks and prior knowledge
          • assessing difficulty of tasks
          • using knowledge of what one knows and needs-to-know to apply more or less effort as needed
            • common pitfall – stopping effort too soon before knowledge is obtained
        2. assessing factors related to academic tasks and how they impact one’s learning
          • setting goals and planning to meet these
          • deciding on standards that will determine success of efforts
        3. selecting cognitive strategies that improve performance
          • changing strategies (if needed) to learn better
        4. major reconfiguration of student’s approach to future tasks based on experience
          • happens rarely
      • multiple phases are iterative in nature
      • types of self regulation processes:
        • Cognitive strategies:
          • practicing, rehearsal
          • organization and elaboration
            • organizing and elaborating on information is more effective than just remembering information
          • deep processing: applying study tactics such as
            • finding relationships between old and new material,
            • rearranging knowledge into meaningful structures (schematic)
        • Metacognitive strategies:
          • self-evaluations
          • goal setting and monitoring
        • Resource-oriented strategies:
          • information seeking
          • record keeping
          • seeking social assistance
          • creating favorable learning environments
    • goal setting
      • setting and regulating monitoring progress towards goals
      • changing approaches to better reach goals
  • Possible effects of learning strategies:
    • increase productivity of academic behaviors -> better academic performance
    • better academic performance -> better sense of self efficacy
    • better self efficacy -> more academic perseverance
    • better academic performance -> enhanced academic mindsets
  • Possible causes of learning strategies:
    • students with academic mindsets are more likely to use learning strategies
  • Possible effects of LACK OF of learning strategies:
    • poor academic behaviors -> poor academic performance
    • students are less likely to complete homework or study for tests when they lack strategies to do these tasks effectively
    • poor grades -> poor academic mindsets -> lessen academic perseverance
  • Possible causes of POOR learning strategies:
    • poor academic mindsets -> less likely to use learning strategies
RELATIONSHIP BETWEEN LEARNING STRATEGIES AND ACADEMIC PERFORMANCE:
  • Students who use self regulation strategies tend to perform better in learning activities / tasks.
  • Students with high self efficacy tend to use metacognition and self regulation strategies more.
  • Self regulation is a strong predictor of academic achievement.
  • Students who perceive learning as understanding (not memorizing) tend to use more strategies to learn.
ARE LEARNING STRATEGIES MALLEABLE?
  • Metacognitive strategies can be learned.
  • Effective metacognitive strategies that can be taught:
    • awareness of textual inconsistency
    • self questioning to monitor and develop comprehension and to make one aware of problem solving steps
  • Use of several metacognitive strategies improved reading comprehension
  • Metacognitive strategies assist with learning at higher thinking levels
  • Teaching learnings strategies in context of a course makes better than teaching them in isolation
  • Transfer of learning strategies to new subjects requires:
    • basis of how strategy works
    • when / where strategy works
    • what it requires of learner
    • the farther the transfer, the more conditional knowledge is needed
  • Math cues that increased metacognition:
    • what is the problem about?
    • what steps would you use to solve this problem
    • these cues helped students draw on prior knowledge, identify problem structures, and evaluate effectiveness of problem solving processes
  • Bootstrapping approach to developing learning strategies:
    • students learn strategies through trial and error or by observing others
    • bootstrapping occurs more in students with academic mindsets
  • Limitation of research = based on self reporting of use of strategies
ROLE OF CLASSROOMS & DEVELOPMENT OF LEARNING STRATEGIES
  • Ways to improve learning
    • paying attention to their thinking as they read, write and problem solve
  • Learning strategies tend to be subject-specific -> content-area classrooms are key places to learn strategies
  • Classroom environments that foster academic mindsets make it more likely for students to apply learning strategies (not enough to simply teach strategies – need mindsets too)
CLASSROOM STRATEGIES THAT PROMOTE LEARNING STRATEGIES:
  • Timely ongoing feedback helps students monitor the effectiveness of their approaches to learning.
  • Self assessments of performance helps students practice metacognitive strategies of self-reflection and critique of learning.
  • Teach subject-specific metacognitive strategies.  See math cues above as examples.
  • Transfer of subject-specific strategies is more likely to occur when strategies are taught in context of a specific subject.
  • Reading specific metacognitive strategies that can be taught
    • recognizing when one doesn’t understand reading
    • using strategies to redirect and refocus comprehension such as
      • rereading,
      • back and forth search strategies,
      • self questioning – comparing text to prior knowledge
      • comparing main ideas of text with details of text
  • Strategies that can be taught:
    • students talk about their thinking as they plan their approach to an academic task
      • paired problem solving – one students explains how they will solve problem while another listens and asks clarifying questions
      • reciprocal teaching – dialog between teacher and students that involves text summaries, question generation, clarifications, and predictions of what till happen next
    • Thinker Tools Inquiry Curriculum
      • Physics curriculum that has students compare virtual experiments to experiments performed on actual objects
      • Encourages metacognition by having students reflect on their own processes of investigation
    • students can learn to identify challenges to academic behaviors and apply appropriate strategies to move forward
    • self regulation strategies that can be taught:
      • mental contrasting – comparing one’s vision for desired future with existing constraints / obstacles that can impede goals
      • implementation intentions – identifying steps to reach one’s goals  written in the form of if statements – if this happens, then I will do this …
      • Applying two strategies above can increase academic perseverance
    • literacy techniques:
      • previewing reading passages
      • restating main ideas in one’s own words
    • test taking strategies:
      • using note cards to quiz themselves
      • making up test questions
      • playing review games
    • goal setting strategies
      • setting aside regular time to set and monitor progress towards goals
CAN LEARNING STRATEGIES CLOSE ACHIEVEMENT GAPS?
  • Very few research studies were designed to investigate gender and race related effects
  • Lack of research is not a proof that this can work
RESEARCH SUMMARY
  • Learning strategies make academic behaviors more effective and more likely -> deeper learning and higher achievement
  • Students with academic mindsets are more likely to apply learning strategies.
  • Classrooms serve 2 key purposes – teach learning strategies and promote academic mindsets
3-sowhat
Teaching learning strategies can encourage students to pursue more effective academic behaviors long enough that they can help students learn.  Teaching subject-specific learning strategies helps students learn content.  Teaching students the underlying hows / whys / whens of specific learning strategies makes them more able to transfer those skills to other disciplines

 

4-nowwhat
Preparation Steps
  • Analyze course and determine subject-specific learning strategies that are key to the success of students in the course
  • Research learning strategies.  See related articles below.
  • Select scaffolding activities that support key learning strategies for course.
  • Create classroom culture that promotes Academic mindsets
Early Implementation Steps
  • Implement scaffolding of learning strategies in the contexts where they are most useful.
  • Ask students to reflect on how learning strategies are affecting their learning.
  • Use student reflections to fine tune scaffolding of learning strategies.
Advanced Implementation Steps
  • Use observations and student feedback on learning strategies to learn which strategies to incorporate into classroom routines.
  • Collect student stories of using learning strategies to overcome challenges in order to inspire future students
5-relatedstuff

135: Assessing Understanding

1-sources

 

2-what

 

Screen Shot 2016-05-09 at 10.47.00 AM

 

  1. Minute Paper
    • Purpose:
      • Assess how well students are understanding content
      • Help make mid-course adjustments
      • Feedback on minute papers helps students distinguish between how experts and beginners distinguish what’s important
    • Description: 
      • Students take 1 minute to answer following questions:
        1. What was the most important thing you learned in class?
        2. What important questions remain unanswered?
    • Suggestions for Use:
      • Assess what students learned from a variety of learning activities
      • Wrap-up or warm-up activities
      • Good for courses that present a great deal of new information
      • Well suited for large classes because it is easy to analyze
    • Example of Implementation:
      • European History
        • Two questions were:
          • What is the single most significant reason why Italy was the center of the Renaissance?
          • What one question puzzles you most about the role of Italy in the Renaissance?
        • Analyzed responses and found that some students were confusing cause & effect
        • Reshaped outline for future activities using student questions
        • Categorized responses by: Major Causes, Minor Causes, Effects, Actors, TBD
        • Answered popular questions
      • Statistics
        • Questions
          • What were the 5 most important points from that session
          • Top 2 questions about the session
        • Compiled lists of responses.  Categorized and tallied similar responses.
        • Responses revealed that students struggles to sort the wheat from the chaff.
        • Showed students top 10-12 responses and discussed their relative importance to each other and the course.
        • Learned to be more explicit in his instruction – example – started providing key points at start of lectures
    • Step-by-Step Procedure:
      1. Decide what to focus on and choose a time to administer assessment that takes place soon after learning activity related to focus item(s)
      2. Write 2 questions – use 2 questions in the Description as a template.  Try out assessment.
      3. Set aside 5-10 minutes to do minute paper and debrief time.
      4. Prepare visual related to 2 questions.
      5. At appropriate time, hand out paper for 1 minute papers.
      6. Suggested – let papers be anonymous.
      7. Let students know their time limits, format of acceptable responses and when the results will be debriefed.
    • Analysis Tips:
      • Tabulate responses and make related useful comments
      • Compare results over time.
    • Extension Tips:
      • Use Half Minute papers – only one question.
      • Make prompt more specific – example – most illustrative example, most compelling charcter, etc.
      • Let students compare and discuss their responses in pairs or small groups
      • Let students in small groups invent own minute paper questions and let members of the group analyze and present results to the class.
    • Pros:
      • Immediate teacher / course feedback
      • Gather questions while time is fresh (and limited) to address them
      • Data can be analyzed and summarized quickly
      • Encourage active listening
      • Shows how teachers value student feedback
      • Feedback on minute paper allow students to compare their responses with the rest of the class
    • Cons:
      • If overused, may seem gimmicky
      • Tricky to come up with questions that can be quickly comprehended and answered
    • Caveats:
      • Technique is flexible but not universally applicable
      • Accept students’ starting points even when they are troubling or irritating.  Don’t develop responses to their paper until frustration (if it arises) subsides.
      • Set flexible time limits for feedback.
      • Promise less feedback than you plan to deliver.
  2. Muddiest Point
    • Purpose:
      • Assesses what students misunderstand
      • Identify which topics need more explanations
      • Requires some higher order thinking
    • Description:
      • Students answer question: What was the muddiest point in ______________?
    • Suggestions for Use:
      • Good for large class sizes because it is easy to analyze
      • Use frequently in classes that present a lot of new information (muddy points accumulate quickly)
    • Example of Implementation:
      • Chemistry:
        • Question: What was the muddiest point in enthalpy versus entropy?
        • Results revealed students had trouble distinguishing between 2 concepts.
        • Showed need for more explicit instruction of each concept in isolation.
    • Step-by-Step Procedure:
      1. Determine which learning activity (or part of learning activity) you want feedback on.
      2. Allow time for students to respond to question at the appropriate time.
      3. Let students know time limit and how responses will be used.
      4. Pass out paper for students to write on.  Collect papers.
      5. Present feedback in next class or soon after.
    • Analysis Tips:
      • Find common muddy points.
      • Divide responses into common categories of muddy points and one miscellaneous pile.
      • Tally responses in each pile.
      • Classify piles as concepts, facts, and skills.
    • Extension Tips:
      • Assign muddiest point to homework assignments
      • Students read each other’s drafts and list muddiest points
      • Ask different groups of students to categorize and summarize responses
      • Followup with other assessment – Directed Paraphrasing, Memory Matrix, Concepts Maps to see if muddy points remain muddy
      • Relate muddy points to upcoming exam questions
    • Pros:
      • Very little prep – can be spontaneous
      • Can be safe outlet for student reluctant to ask question in class
      • Can help teachers identify what students find hard to learn – help set different focus for future learning activities
      • Get in students’ shoes
      • Can help students become more metacognitive
    • Cons:
      • Can undermine motivate and sense of self efficacy – can combat that this by teaching students the value of struggles and mistakes
      • Can be discouraging to know what students misunderstand in a well-prepped learning activities
      • Students may struggle to identify and describe their struggles
      • Students may raise challenging questions that are hard to answer on the spot
    • Caveats:
      • Don’t express anger or disappointment when students list muddy points that you thought you explained well
      • Don’t spend too much time responding to muddy points – may lose course momentum
      • Don’t convey that all muddy points can be resolved quickly – some are landslides that take a lot of time to uncover
3-sowhat
The Minute Paper and Muddiest Points are easy-to-analyze assessments of student (mis) understanding.  These can be used to give teachers immediate feedback on the effectiveness of learning activities and insights on how to refine upcoming activities.

 

4-nowwhat
Preparation Steps
  • Decide opportune times for students to summarize what they know (or don’t know) using Minute Paper or Muddiest Point.
  • Decide how you will quickly analyze and summarize the data and how you will use that data summary.
Early Implementation Steps
  • Assign Minute Paper or Muddiest Point
  • Analyze and summarize the assessments.  Decide how to make adjustments that highlight student understandings and resolve student misunderstandings.
  • Share results with students with students and how these will impact instruction and student learning.
Advanced Implementation Steps
  • Involve students in the writing of Minute Paper & Muddiest Point questions and in the analyze and summarization of results.
  • Have students reflect on how their understanding of muddy points is improving (or not) over time.

 

5-relatedstuff

134: Assessing Recall

2-what

 

Screen Shot 2016-05-09 at 10.59.25 AM

 

  1. Focused Listing
    • Purpose:
      • Assessing what students recall in regards to a specific topic
      • Improve students’ focus and recall
    • What It Is: 
      • Students list several ideas that relate to a focus topic
    • Suggestions for Use:
      • Can be used before, during, or after a lesson
      • Simple assessment that can be used in many classes
      • Good for courses that involve a lot of new information
    • Example of Implementation:
      • Physics:
        • Used to assess students’ understanding of vocabulary such as “work” (2 min exercise per list)
        • Divide into 3 piles: mostly current, confused with everyday meanings of words, the rest
        • Includes concepts and student wording into lesson on work – especially when differentiating between everyday and physics definitions of work
      • Finance:
        • List 5-7 fundamental concepts related to “stocks”
        • Briefly define each concept (10 min exercise)
        • Analyzed sheets to see what was present and missing from students’ lists
        • Following class meeting handed out printed sheet with concepts and definitions and reviewed 3 fundamental concepts not found in sheets
        • From then on, prior to lessons – listed few topics to key in on during upcoming lesson
      • Political Science
        • Prior to a lesson on Federalism handed out 3×5 index cards
        • Wrote BEFORE on one side of cards and listed topics related to Federalism
        • Near end of lesson, wrote AFTER on back of cards and listed more topics related Federalism
        • Gathered top 3 topics from each students
        • To respond to wide variation in topics, at start of next lesson showed student visual that included
          • all 23 topics mentioned by students organized into 6 categories – top 5 fundamental ideas and Other
          • Also organized topics in a concept map
    • Step-by-Step Procedure:
      1. Select important topic currently being studied in class.
      2. Write topic at top of a blank answer sheet.
      3. Set time and/or list item number limits.
      4. Following own time limits, create sample focus list.
      5. Revise list, add items as needed.
      6. If list is well defined and worth discussing, run the same exercise with your class.
    • Analysis Tips:
      • Compare students’ lists to your list and divide into piles: Appropriate, Inappropriate Or Related / Unrelated
      • Categorize responses by relationship to the focus topic – examples: definitions, examples, descriptions, illustrations, primary, secondary, tertiary relationships to focus topic
    • Extension Tips:
      • Allow students to work in small groups to develop collective focus lists
      • Make your focused lists available for comparison and discussion in class
      • Have students in small groups create compiled lists that contained best items from their lists and your list
      • Ask students to define terms on their lists
      • Have students convert into paragraph(s) that relates terms to each other and focus topic
      • Use Focus List strategy at regular intervals to increase recall and prioritization of content
      • Follow-up this strategy with Empty Outlines activity – see below
    • Pros:
      • Simple, quick and flexible way to measure student recall
      • Identify terms students recall and don’t
      • Time limits have students list what they perceive to be the key terms, not what they think the teacher wants
      • If used before instruction, can be used to prime the pump, ready the brain for new learning
    • Cons:
      • Basic form only assesses low cognitive skill, recall
      • Some students can product reasonable lists without really understanding terms
      • Focuses on one idea at time – some key knowledge focuses on relationships among several key concepts
    • Caveats:
      • Create your own master focused list to trial key topic prior to assigning focused list.
      • Focus lists on key big ideas (enduring understandings).
      • Pick a topic that is not too broad or too narrow to create a somewhat convergent variety of lists.
      • Add specifics about relationship between focus list words and focus topic – examples, defining words, synonyms, examples, etc
  2. Empty Outlines
    • Purpose:
      • Assess students’ recall and note-taking skills
      • Emphasizes key topics and their sub-topics
    • What It Is:
      • Students complete an empty or partially completed outline – if partially completed, include key headings and empty spaces for sub-topics
    • Suggestions for Use:
      • Good for courses that have a lot of detailed information that are highly structures
    • Examples of Implementation:
      • Nursing Course
        • Provided students with outline with 4 major topics and empty slots for 5-7 subtopics for each major topic
        • Students completed outlines using their notes
        • Teacher compared outlines to her lecture outline
        • Uses disparities in the prioritization in her notes and her students’ notes to learn how to better emphasize key points in future lectures
      • Child Development Course
        • Prior to showing a video to a class, teacher watched the video and created outline of video contents
        • Created empty outline by deleting sub-headings and keeping major headings
        • After students watched the video, gave students 5 minutes to complete the empty outlines in pairs
        • Found that their notes coincided with his notes at the beginning and end of the video and deviated most near the middle of the video
        • In the future, paused video in the middle to give students time to take notes
    • Step-by-Step Procedure:
      1. Create an outline for an upcoming learning activity.
      2. Decide what info you want students to provide – major topics, sub-topics, supporting details etc.  Let that inform empty outline design.
      3. Limit number of blank items for students to complete on empty outlines to less than 10. (if you want them to complete it from memory)
      4. Communicate expectations – time limits and types of things to put in empty outlines
      5. Convey purpose of assignments, when results will be shared, and how results will be used.
    • Analysis Tips:
      • Compare student outlines with your outline and learn from agreements and disagreements
      • Look at range of responses and notice patterns in responses
    • Extension Tips:
      • If students struggle to complete the outline, provide a word/phrase bank.
      • Vary between providing major subtopics and asking for supporting details and providing supporting details and asking for major topics.
      • For advanced students, provide guidelines only
      • Use focused listing activity prior to completing outlines – use focused list items in outlines
      • Do outline as a warmup to see student expectations for a lesson
    • Pros:
      • Repeated use can improve student listening and note taking.
      • Feedback on outlines gives students better models for note taking.
      • Can help students better organize knowledge in their notes and in their brains.
      • Can make organizing ideas of a subject more explicit
    • Cons:
      • May feel constrained by the master empty outline
      • Not all information is best organized in hierarchical structure of outlines
      • Unless students make outlines from scratch, little higher order thinking is required
    • Caveats:
      • Students’ varied readiness levels will lead to variation in their empty outlines
      • Limit amount of info captured in empty outlines (less than 10 points)
  3. Memory Matrix
    • Purpose: 
      • Assess recall and organization of important information
    • What It Is:
      • Students complete a chart that has row and column labels that emphasize key relationships between ideas
    • Suggestions for Use:
      • Works well with subjects with a lot of detailed information that relates to each other
      • Can assess recall of information after a variety of learning activities
      • Can be used as a pre-assessment
    • Example of Implementation:
      • Spanish:
        • Gave students a matrix to complete that had types of verbs (-ar, -er, ir) as the column headings and (regular/irregular) as the row headings
        • Found that students sometimes classified regular verbs as irregular verbs and confused -er and -ir verbs
        • Info help teacher decide to review in upcoming classes
      • Art History:
        • Gave students a matrix with column headings: France, US, and Britain and rowing headings: Neoclassicism, Impressionism, Postimpressionism, Expressionism.
        • Students completed matrix in groups of 5; then transferred responses to a whole class chart
        • Students could categorize artists by country but struggled to separate them by time period
        • Use their misconceptions as a starting point for upcoming lectures
      • Nursing class:
        • Gave students a matrix with column headings: structure, functions, enzymes and row headings: mouth, esophagus, etc (other digestive system organs)
        • Students completed matrix in teams of 5
        • While students watched a video on enzymes he analyzed the students’ matrices.
        • Using model matrix, he reinforced what students got right and discussed what students got wrong.
        • Then gave individuals another blank matrix and had them complete it at class end.
    • Step-by-Step Procedure:
      1. Draw simple matrix with row and column labels that represent key topics in the course.
      2. Create a key based on learning activities.
      3. Revise Memory Matrix if needed – check for fit of row and column labels to key ideas.
      4. Create a blank version of Memory Matrix that only has row and column labels.  Make blank cells large enough to record several ideas.
      5. Give students time to complete the matrix.  Set a lower limit for the number of items in each cell.
      6. Analyze matrices for correctness.
    • Analysis Tips:
      • Analyze correctness of matrices and look for trends in correctness and incorrectness to identify student strengths and gaps.
      • Analyze errors and look for patterns in the errors.  Use this diagnose amount of learning time & type of activities associated to each topic.
    • Extension Tips:
      • Complete Memory Matrix as part of a class discussion.
      • Allow students to work in groups on the matrix.
      • Fill in some of the middle cells and have students guess the rowing headings or column headings.
      • Give students a Work/Phrase Bank and have them create the Memory Matrix (complete with original row and column headings) that organizes the terms in the bank
    • Pros:
      • Assess recall of information and how well students can relate information
      • Simplicity of format makes it easy to analyze
      • Graphic format may appeal to visual learners
      • Can improve memory organization and retrieval
    • Cons:
      • Row and column headings impose organization formats that may hide organizational relationships students are using to relate content
      • Basic format of assessment may not separate prior knowledge and current knowledge well
      • Can obscure flexibility and complexity of the actual relationships among content
    • Caveats:
      • Start with small matrices (2×2) for students unfamiliar with this strategy.
      • May obscure relationships that are flexible / blurred.  Need to point out these nuances in learning activities.
      • Recognize matrices as a convenient simplification of a more complex reality
3-sowhat
All 3 of the strategies in this article assess student recall and assess relationships students see among the information items they recall.  Providing feedback on these items can provide opportunities to make priorities and relationships among content more explicit.  Varying the format for the recall assessments can emphasize different relationships.  The Focused List assessment shows how one central idea relates to sub-ideas or supporting evidence.  The Empty Outline can show how several central ideas relate to other pieces of information.  The Memory Matrix shows how 2 groups of ideas (categories) can be used to show relationships between detailed pieces of information.

 

4-nowwhat
Preparation Steps
  • Analyze the knowledge and skills in the standards in the upcoming standards.  Look at the key relationships you’d like to teach to students to students among major and supporting ideas.
  • Decide which type of recall assessments best illustrates the relationships you’d like students to use to organize ideas in upcoming learning activities.
  • Prepare samples / keys for the selected strategies you will use.
Early Implementation Steps
  • Ask students to work on assessment(s) individually or in teams.
  • Analyze assessments.  See above for tips.  Try to learn student strengths and gaps and what are the patterns in their strengths and gaps.
  • Use what is learned from assessments to modify instruction.
  • Share results with students and how results will impact upcoming instruction and student learning.
Advanced Implementation Steps
  • After students have had practice with the recall strategies – try extension version of the activities.  See above.
  • Incorporate a recall strategy into classroom routines – pick one that emphasizes skills and organization styles that fit well with your course.
5-relatedstuff

131: Rich Mathematical Tasks

1-sources

 

2-what

 

Screen Shot 2016-05-09 at 11.19.42 AM

 

5 C’s of Mathematical Engagement:
  1. Curiosity
  2. Connection making
  3. Challenge
  4. Creativity
  5. Collaboration
Why Rich Mathematical Tasks:
  • expose people to openness and flexibility of mathematics
  • generate excitement
  • create more opportunities for understanding
  • provide support for high challenge tasks
Characteristics of Engaging Lessons with Rich Mathematical Tasks
  • Task is challenging (high ceiling), but accessible (low floor).
  • Students view task as a puzzle
  • Visual thinking builds understanding
  • Classroom culture values mistakes
  • Students respect each other’s thinking
  • Students use own ideas (not blindly follow given procedures)
  • Students collaborate
  • Students have different things to offer to team effort to solve problem
  • Students don’t think they are finding a standard answer – think they are finding own solutions to a problem
  • Good Timing (Just in Time Teaching)
    • Let students explore applied problems first
    • Observe students
    • Introduce methods when they reach a stuck point that can be resolved by the method
    • Helps students learn value of methods and develop intuitive sense for methods
 
Examples of Rich Mathematical Tasks:
  • 18×5
    • Solve 18×5 using mental math
    • Display different solutions using simple thumbnail sketches
  • Growing geometric patterns
    • Explain visually how pattern is growing
    • Share different growth pattern ideas
    • Use growth pattern ideas to find 100th and nth iterations of patterns
  • Build a fence out of 36 1-m planks
    • Use 36 1-meter planks to build fence that encloses the most land
  • Lemon volume
    • Find the volume of a melon (precursor to teaching integration methods)
  • Cuisenaire Rod Train Task
    • Use Cuisenaire Rod to determine how many different trains can be made from a rod of prescribed length
    • Find connection between Pascal’s triangle and numbers of trains in rods
  • Negative Space Task
    • Find patterns in geometric patterns that go up in positive indexes and then down in negative indexes
    • Figure out how to represent negative index results visually and numerically
  • How Close to 100?
    • Roll pair of dice – use pair of dice to draw an array on a 10×10 grid.  Write number sentence that related dice numbers to array area,
    • Take turns rolling dice, drawing arrays and writing related number sentences
    • Place until no more arrays can be fit unto 10×10 grid
  • 1 Divided by 2/3
    • Don’t apply the fraction rule of division
    • Use visuals to make sense of answer
  • Four 4’s
    • Make all numbers from 1 to 20 using four 4’s and any operation
    • For tips on how to stage this lesson, go here
  • Paper Folding – Use paper folding of a square piece of paper to do the following
    • Construct a square with exactly 1/4 the area of original square – convince partner that it is 1/4 the area
    • Construct a triangle with exactly 1/4 the area of original square – convince partner that it is 1/4 the area
    • Construct another triangle with exactly 1/4 the area of original square that is not congruent to the first triangle – convince partner that it is 1/4 the area
 
Developing Rich Mathematical Tasks: Questions to Consider:
  • Open the task encourage multiple methods, pathways and representations.
    • Add visual requirement
    • Ask students to make sense of solutions
  • Make it an inquiry task.
    • Ask students to come up with ideas, not follow a procedure
    • Create products about solutions (brochure, newsletter, etc)
      • examples
        • write a book about y = mx + b
        • create a coffee table book about similarity
  • Ask the problem before teaching the method.
    • Introduce methods after students have developed methods that relate or approximate new methods or after students reach a stuck point that can be unlocked with new method
  • Add a visual component.
    • Use drawings, math manipulatives, etc to represent solutions and ideas
    • Use color coding to feature common features in solutions such as “x” or to highlight relationships
  • Extend the task to make it low floor and high ceiling.
    • Low floor – ask students how they see the problem
    • High ceiling – ask students to write a new question that is similar but more difficult
  • Add the requirement to convince and reason
    • Explain methods and why they make sense
    • Reasoning is practicing mathematics
    • Reasoning gives access to understandings that can close equity gaps
    • 3 levels of convincing
      1. Convince yourself
      2. Convince a friend
      3. Convince a skeptic
 
Suggested Reading & Related Resources
3-sowhat
Rich mathematical tasks can be used to engage all students in mathematical solving and sense making.  The principles behind good design for these tasks can be used by teachers to frame problems and lessons that invite students to apply their own ideas to problems and to relate these ideas to new concepts and methods.

 

4-nowwhat
Preparation Steps
  • Analyze standards and develop learning targets related to concepts and problem solving methods
  • Use resources above to find rich and engaging mathematical tasks that relate to learning targets
  • Build scaffolding and assessments around rich mathematical tasks that align to learning targets
Early Implementation Steps
  • Use rich mathematical tasks to:
    • create engagement
    • introduce new concepts
    • help students see need-to-knows in new content
    • make sense of new content
    • to get students to discuss their reasoning
  • Use assessments to fine tune activities to improve student learning
  • Ask students to reflect on how activities are improving their learning
Advanced Implementation Steps
  • Build a bank of rich mathematical tasks that goes with a course’s scope and sequence
  • Find rich mathematical tasks inspired by nature and the real world
  • Recruit stakeholders to serve as clients for students solving rick mathematical tasks

 

5-relatedstuff

130: Creating Mathematical Mindsets

1-sources

 

2-what

 

Screen Shot 2016-05-09 at 11.29.38 AM

 

Mathematical Mindsets – What They Are:
  • Present naturally in children who like to inquire, build things, solve puzzles, notice/make patterns, etc
  • Seeing math as a conceptual subject that they can grow to make sense out of
  • Stepping forward deliberately and deeply in math while making sure each step makes intuitive sense before moving more forward
How to Stunt Development of Mathematical Mindsets:
  • Presenting math as a dry set of methods can stop development of mathematical mindsets
    • this is especially true if methods do not make intuitive sense to students
  • Presenting math as seires of short questions obscures growth opportunities – math is something you get or you don’t, instead of something to make sense of
  • Assigning large homework sets with simple isolated problems
  • Valuing rote memorization and speed over deep thinking and conceptual understanding
How to Develop Mathematical Mindsets:
  • Encourage students to play with numbers, shapes and puzzles
  • Present math as a broad landscape of unexplored puzzles that create opportunities for wandering around, asking questions, thinking of relationships, …
  • Present math as a flexible conceptual subject that is about thinking and sense making
  • Be mindful when designing practice set because mindless practice does not lead to brain growth, thoughtful practice does – mindful practice involves applying same strategy to many different situations
  • Assign less homework that requires more reflection – example 5 carefully selected problems and one student chosen reflection question such as:
    • What are the main mathematical ideas we discussed in class today?
    • What questions do you have about ________?
    • Describe a mistake or misconception you or a student had in class today.  What did you learn from this mistake or misconception?
    • How did you approach your practice set? Was your approach successful? What did you learn from your approach?
  • Cultivating Number Sense:
    • Approach arithmetic operations flexibly and conceptually:
      • concept of sum -> counting on
      • concept of product -> repeated addition
    • Try to help students make sense of concepts and patterns so that their brain can more readily go from compression – more efficient storage of concepts (not rules)
    • Math facts are stored in working area of brain – this area can be blocked when students are stressed
    • Avoid techniques that value speed of knowing math facts (example – timed tests)
    • Do NOT emphasize rote knowledge and speed – gets in the way of thinking about numbers and their relationships to each other
    • Teach strategies instead of memorization of facts
      • example: 17 x 8
        • strategy – 17 x 10 – 17 x 2 = 170 – 34 = 136
        • memorize 17 x 8 = 136
    • play math games that  activate both sides of brain by using visual and intuitive math thinking:
      • example: grid multiplication game
        • object of game – fill as many grid squares as possible in a 10 x10 grid
        • roll 2 number dice – color in area that corresponds to product of 2 numbers rolled and write number sentence
        • partners take turns rolling dice, coloring in areas and writing related number sentences until no more arrays can be added to the grid
      • example: multi rep matching game
        • players take turns picking pairs of equivalent cards and explaining why they are equivalent
        • find cards and more cool strategies here
    • Do “Number Talks” as warmups
    • Recommend math games that emphasize concepts over drill & kill:

 

3-sowhat
Developing mathematical mindsets will help student approach mathematics with a growth mindset.  Mathematical mindsets help students understand math concepts more deeply and apply them more flexibly.  Valuing conceptual understanding over speedy rote memorization is one way to cultivate mathematical mindsets.

 

4-nowwhat
Preparation Steps
  • Research more strategies for developing mathematical mindsets.  See Mathematics articles for ideas.
  • Develop lesson plan components (Warmups, practice sets, discussions, activities, etc) that promote mathematical mindsets
Early Implementation Steps
  • Regularly use scaffolding and assessments that promote mathematical mindsets
  • Have students reflect often on what they are learning
    • about concepts
    • about how concepts are applied to problem solving
    • from mistakes
    • from different problem solving approaches
Advanced Implementation Steps
  • Have students interact with mathematicians and professionals who apply mathematical reasoning often and learn about their problem solving approaches
  • Develop bank of Number Talk problems and games that promote mathematical mindsets and incorporate these into classroom routines
5-relatedstuff

129: Creativity & Beauty of Mathematics

1-sources

2-what

Screen Shot 2016-05-09 at 11.36.48 AM

 

Traditional School Math & Math Misconceptions
  • Math is hated/feared because it is taught and thought of in ways that are different from other subjects.
  • Primary role of students in traditional math classrooms is to perform and get questions right.
  • Performing takes precedence over learning.
  • Testing culture promotes idea that math is about finding short answers to narrow questions under pressure.
  • Math is a subject of procedures, calculations and rules.
  • Math is a dead subject that is only present in textbook calculations.
  • Math is a series of answers to questions that nobody asks in the real world.
  • Math in classrooms focuses primary on Stage 3 of math stages (see below)
  • Student shouldn’t have to show work if their answer is right.
  • Math is done by individuals.
  • People who are good at math perform calculations QUICKLY.  Math is a speed race.
 
Real Nature of Mathematics
  • Besides getting question right, doing math involves:
    • appreciating beauty of math
    • thinking deeply
    • exploring math connections
    • applying math to different situations
    • exploring patterns
    • using math to create and analyze new technology and strategies
    • formulating questions
  • Math exists throughout nature, art, and the world.
  • Nature contains many examples of mathematics
    • spiders are experts in spirals
    • dolphins use a form of algebra to interpret echolocation signals
  • Instead of study of procedures, calculations and rules, math is
    • study of patterns (aesthetic, beauty of subject)
    • subject of visual images, creativity and connections
    • subject that is full of uncertainty – answers can be explorations, interpretations, conjectures
    • set of ideas, connections and relationships that we can use to make sense of the world
  • 4 Stages of Math Work
    1. Posing a question
    2. Going from real world to a mathematical model
    3. Performing a calculation
    4. Going from model back to real world to see if original question was answered
  • Real math is often done collaboratively
  • Speed of calculations has nothing to do with math fluency.
 
How to Align Math Schooling with Real Mathematics
  • Give students opportunities to consider situation and formulate math problems to investigate these situations
  • Give students opportunities to use all 4 math stages
  • Require students to show work because displaying logical mathematical lines of reasoning is the main part of doing math
  • Facilitate math discussions about mathematical reasoning (what it is, how to critique and justify it)
  • Pose open-end problems and allow students to develop methods and pathways to solutions
 
Workforce Implications
  • Employers need people who can ask good questions, set up models, analyze results and interpret mathematical answers.
  • Employers no longer need people to calculate; now they need people to think and reason
3-sowhat
Math misconceptions have crept into the design of math curricula.  These math misconceptions have made the subject appear uninteresting and unappealing to some.  Knowing the true nature of mathematics can help teachers design learning experiences for students that are engaging, challenging and relevant to the real world.

 

4-nowwhat
Preparation Steps
  • Research more methods for designing learning experiences that are more true to the math discipline.  See Mathematics articles.
  • Research strategies for 4 Phases of Math (see above).
  • Create a culture that values mistakes.  See this article for ideas.
  • Design scaffolding that includes elements such as:
    • balance of 4 phases of math
    • facilitated math discussions about mathematical reasoning
    • pattern recognition
    • students posing questions and possible solutions
    • student creating models for the real world
Early Implementation Steps
  • Implement scaffolding that provides students with many opportunities to appreciate and practice real mathematical thinking
  • Have students reflect on how their math attitudes are changing as a result of math activities that deliberately mimic the math discipline
Advanced Implementation Steps
  • Provide students with opportunities to solve real world problems using math
  • Provide students with opportunities to interact with real world stakeholders in order to pose better questions, formulate better models, learn better calculation methods and compare/interpret their results to real situations
  • Try to brainstorm what math looks like when mapped unto the 6 Facets of Understanding and Bloom’s taxonomy

 

5-relatedstuff